Previously, we talked about what composite materials are, in an engineering sense. To recapitulate, composites are materials comprising two or more constituents. The constituents are combined in a way such that they retain their distinct identities in the final material (unlike alloys, for example). In particular, we talked about composites with a homogenous ‘matrix’ material (such as epoxy resin in polymer composites, and metals such as aluminum in metal matrix composites) in which reinforcing fibers (such as carbon fibers or glass fibers) or particulates are embedded. The fibers are the reinforcing material that provides strength to the composite, while the matrix material serves other purposes such as: (a) protecting the fibers (b) binding the fibers together to actually create the composite (c) helping to redistribute stresses if a fiber breaks.

But the key question is: why use composite materials at all? Why not use metals as always? What advantages do composites provide? Turns out, quite a few.

For one, composites are stronger than traditional industrial materials. How is strength measured? We all intuitively know this—by the amount of load that a material can withstand. Of course, for a fair comparison, the area over which the load (force, in technical parlance) is applied must be the same. (A thicker piece of wood carries more load than a thinner piece, but the wood itself remains the same strength; only the area of loading—the thickness, in this case—changes.)

A Mercedes-Benz bicycle that has a composite frame. (Source)

For another, most composites are lighter than their traditional counterparts. This is measured by density, which is the weight of the material per unit volume (just like we had considered constant area in the case of force, we must consider constant volume when considering weight). Like the example before, a larger piece of wood weighs more than a smaller piece, but the density of the wood itself remains the same.

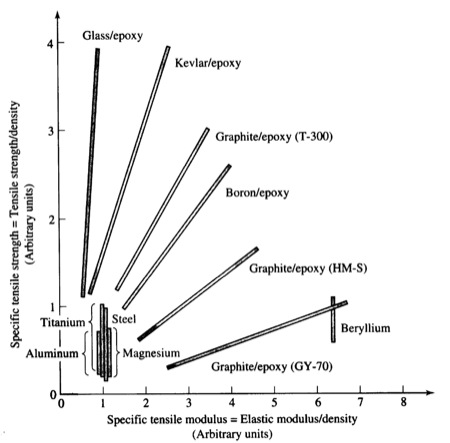
Comparison of material properties, normalized by density. (Longer is better. Notice the metallic materials at bottom left.) (Source)

Combine the two traits—lighter and stronger—and what we get is a material that can withstand the same load with a smaller amount of material, and the material itself weighs less for the same volume! This is a pretty neat arrangement, no?

It doesn’t end there; this is just the beginning.

–

Remember, most of the strength of a composite material comes from the fibers in the composite. Now consider a composite with all the fibers parallel to each other, i.e. pointing in the same direction. In which direction (or directions) does the composite have the most strength? Is it equally strong in all directions? Evidently not—the fibers provide tensile strength along its own direction, and so the composite itself will be much stronger in the ‘fiber direction’ as compared to other directions. We’ve discussed wood as an example before, and you’ll notice that the situation is very similar to this case of unidirectionally arranged fiber-reinforced composites.

Load on a table top: notice the fiber direction! Here the requirements are bending strength for the table top, and ability to transfer the load to the legs of the table. (Source)

Now that we’re comfortable with the idea of a unidirectional composite, consider this material as a building block. If you had a unidirectional material, that you could orient any way you like, and stack them so that the final material had fibers in multiple orientations, could you design a material to be strong in any direction you wanted? Certainly you could! And this is exactly what is done.

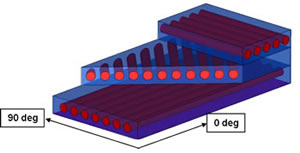
Composite Ply Layup. (Source)

And this brings us to the engineering and design side of composites. Even though, at first look, this seems like a dubious idea—isn’t it better that the things we make are equally strong in all directions? What if it breaks in one of the weaker directions?–this makes good engineering sense. Whenever a new component is designed, the designer has already figured out what the weak points of the structure are, and has already planned a way (or ways) that the component should fail, should it become overloaded or reaches the end of its life. In other words, a good engineering design factors in, during the design process, the directions that the component needs to be strong in, and the ways the material can and should fail.

Of course, this implies that the components perform at their best when they are used as intended. If a golfer strikes his golf club in frustration against a tree trunk, should he be surprised if his prized club goes out of shape? (On the other hand, if many golfers do this exact same thing, the designer of the hi-end golf club might take this into consideration when he makes a new design—but it probably will make the club even more expensive!)

A bent golf club, after it was struck against the ground. (Source)

And of course, what of the case where the component does actually need to be equally strong in all directions? Well, there’s nothing preventing the designer from using plies oriented in all directions, right? A component where the fibers are oriented so that the properties are approximately the same in all directions is called a quasi-isotropic material, i.e. a material that behaves sort of like an isotropic material, even though it actually isn’t.

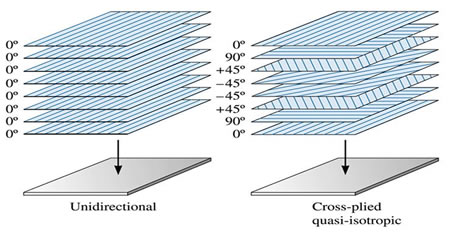
A unidirectional and a quasi-isotropic laminate. (Source)

One final thing for this session. How to describe the ply sequence of composites? In brief (I’ll clarify as we come across actual examples), the most basic nomenclature is just a sequence of the play angles, with one of the fiber directions designated the ‘zero degree’ direction. Since it can get cumbersome to write the sequences of multi-layer composites (consider a 16-ply or 32-ply laminate, for example!), symmetries and repetitions in the order of the plies is used profitably. The subscript ‘S’ denotes symmetry, ‘N’ (where N is a number) denotes N repetitions of the same order, and ‘T’ conveys that no symmetries and repetitions are present (i.e. it is the ‘total’ sequence). Please see the figure below for some examples.

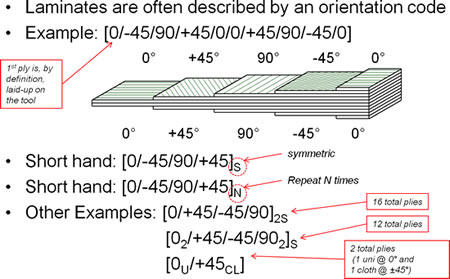
Composite stacking sequence nomenclature. (Source)

To summarize, the advantage of composites is first in its most basic properties—it is both stronger and lighter than traditional metallic materials. (It must be noted that this is a simple generalization; ‘strength’ can be of various kinds. For example, composites are usually not very good in compression). Further, composites can be engineered as per design requirements of each component. A basic unidirectional building block can be used to prepare composites with a variety of effective material properties.

In the broadest sense, a composite material is one that consists of two or more distinct materials—which retain their individual properties even when the final material is formed! In fact, we’ve all encountered various composite materials in our everyday lives.

Aggregate Concrete. (Source)

Take concrete, for example. Have you ever seen concrete being made for construction? It comprises cement (which binds everything together) and many other materials, including crushed stones. The properties of concrete are a combination of the properties of everything that went into it. Moreover, if concrete in its finished form is seen under the microscope, one finds that the components are essentially “mixed in”, and don’t interact chemically with each other in any way.

(This is, in contrast, to things such as alloys. Alloys, for example, are also made of multiple components—mostly metals, sometimes nonmetals such as carbon—but the final product has vastly different properties than the constituent materials. Also, the components themselves interact with each other at the smallest scale, and are not simply “mixed together”.)

Plywood is another example of a common composite material. In this case, you don’t even need a microscope: the individual layers making up the plywood are evident quite easily! In fact, while we’re on plywood, let’s remember the word ply—it refers to each layer of wood that makes up the plywood (yes, that’s how it gets its name). We’ll use the word ply plenty times later on.

Plywood. (Source)

Okay, so that’s what composites are in the broadest sense.

But in an engineering and research perspective, a “composite” is something more specific. To wit, a composite material is an engineered material, in which one or more heterogenous components are used as reinforcement in a matrix of homogeneous material. If the material used as a matrix is a metal, it’s called a Metal Matrix Composite (MMC).

Okay, so let’s break that last paragraph up a little bit. First, the “matrix of homogeneous material”. This refers to any material that’s uniform (like cloth, gauze), which serves as the base for your composite, and between layers of which—or even into which—you can embed other things if you wanted to. (In concrete, the cement can be thought of as the matrix, into which you can add other things—including steel rods to create reinforced concrete!)

Reinforced Concrete. (Source)

As I already said, if the matrix material is a metal, the composite is called an MMC. But a variety of other materials are also used as the matrix material—different kinds of polymers, usually. The most popular one that I’ve come across is epoxy resin, but other than that, vinylester or polyesters are also used.

The reinforcing material in the composite is usually either a fiber (more common) or a particulate material (less common). Since fiber-reinforced polymers are more common—and what I mostly work with—let’s talk about fibers a little bit.

Fracture surface of a SiC fibre-reinforced Cu metal matrix composite. (Source)

Fibers are a source of strength in composites, and a number of different kinds of fibers are used. Most common are carbon fibers, glass fibers, or even boron fibers. The question, of course, is—if the fibers add strength, why not build the entire material out of the same material as the fiber? Well, due to the way materials are manufactured, larger the size of the building block (i.e. the smallest unit used over and over again), lower is the overall strength. Hence, for example carbon in fiber form is much, much stronger than carbon in, say, sheet form (interested readers should look up “carbon fiber whiskers”–I could not find appropriate web pages to link to). This is why fibers are used for strength, and other materials (the matrix) are used to hold everything together around the fiber. (One can think of Metal Matrix Composites as special cases where even the matrix needs to be strong in its own right.)

Thus, to summarize, a composite material usually comprises a homogeneous matrix material, in which certain fibers are embedded to add strength and other advantages to the material. In some cases the matrix can be a metal, in which case the overall material is even stronger.

Let us get introduced, first, to a class of materials which are highly directional in nature. What does directional mean? Let me give an example. Imagine that you have a sheet of thermocol in your hand. Try to pull the sheet apart—if it’s thin enough, you probably can. Does it matter in what direction you hold the sheet of thermocol? Top-bottom versus left-right? Of course it doesn’t. This is an example of a material that is not directional—it responds in identical fashion, whichever direction you choose to interact with it in.

Thermocol Sheets. (Source)

Now consider a log of wood. Have you seen pieces of wood closely? Have you noticed the striations that seem to run along the length of long pieces or logs of wood? Those are natural fibers present in the wood, and they provide the wood extremely high strength on the direction of the fibers. It’s pretty hard to cut wood across those fibers, and wherever possible, wood is cut along those striations.

Wood Grain. (Source)

Wood, then, is an example of a material that’s directional—its response to external effects (such as a saw cutting through it) differs along different directions. That brings us to our first set of technical terms: isotropy and anisotropy. The thermocol sheet (or Aluminum, or Steel, or most other metals) is not directional—it’s isotropic. Wood is directional—and is anisotropic.

Why is this important? Because composite materials gain significance in large part because they’re anisotropic! Which means, they’re strong in one direction; not-so-strong in another. Plus, they can be engineered to be strong in any direction you want!

Boeing is in the process of launching (finally, after delays) its latest aircraft, the Boeing 787 Dreamliner. This is the first new major jet launched since the Airbus A380, and of course, has me interested in many ways.

Of course, on a personal-professional level (if that term makes any sense, which I have a feeling it doesn’t—anyway, I work with composite materials, remember?) the B787 is mostly made out of composites. Mostly out of carbon-fiber laminates; some out of carbon fiber sandwiches—use of metal (titanium and aluminum) is minimal.

Second, I just love the wing design. The sweep and curve upward of the wings is just beautiful. Also, it is a vast improvement over the last generation of wing-tips, which looked as if from a design perspective they were a later ‘add-on’ to a previous, flat shape. Here, finally, is a smooth, elegant, downright beautiful wing shape!

I also found this link to the B787’s design highlights. It’s an informative page, do check it out. (For information about the composites being used, go to Visionary Design→Composites.)

From the link above, I learn (among other things):

• There is a very futuristic HUD (Head-Up Display) in front of the pilots which combines what the pilot actually sees with other useful information that the pilot needs. I’ve seen things like these in Fighter Aircraft simulations, but is this the first time it’s being used commercially?
• The B787 is not a very large aircraft! I had inherently assumed that the plane would be B747 or A380 scale (i.e. a pretty big plane), but it’s not—it can carry a maximum of about 300 passengers, compared to the B747’s ~400 and the A380’s 525 in three classes.
• The internal air pressure of the aircraft will correspond to a lower altitude (6000ft, as compared to 8000ft in earlier aircraft), and will have higher moisture content—meaning a more comfortable flight!

Now, what remains is for the major airlines to buy these and put them into service.