Previously, we talked about what composite materials are, in an engineering sense. To recapitulate, composites are materials comprising two or more constituents. The constituents are combined in a way such that they retain their distinct identities in the final material (unlike alloys, for example). In particular, we talked about composites with a homogenous ‘matrix’ material (such as epoxy resin in polymer composites, and metals such as aluminum in metal matrix composites) in which reinforcing fibers (such as carbon fibers or glass fibers) or particulates are embedded. The fibers are the reinforcing material that provides strength to the composite, while the matrix material serves other purposes such as: (a) protecting the fibers (b) binding the fibers together to actually create the composite (c) helping to redistribute stresses if a fiber breaks.
But the key question is: why use composite materials at all? Why not use metals as always? What advantages do composites provide? Turns out, quite a few.
For one, composites are stronger than traditional industrial materials. How is strength measured? We all intuitively know this—by the amount of load that a material can withstand. Of course, for a fair comparison, the area over which the load (force, in technical parlance) is applied must be the same. (A thicker piece of wood carries more load than a thinner piece, but the wood itself remains the same strength; only the area of loading—the thickness, in this case—changes.)

A Mercedes-Benz bicycle that has a composite frame. (Source)
For another, most composites are lighter than their traditional counterparts. This is measured by density, which is the weight of the material per unit volume (just like we had considered constant area in the case of force, we must consider constant volume when considering weight). Like the example before, a larger piece of wood weighs more than a smaller piece, but the density of the wood itself remains the same.
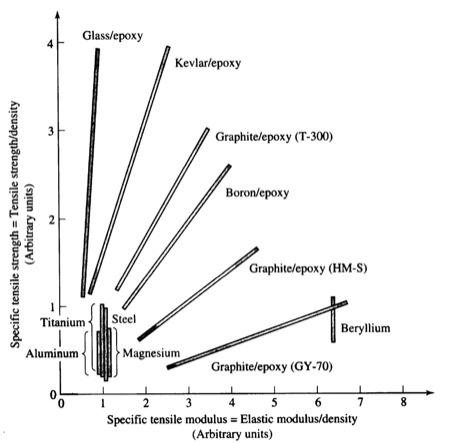
Comparison of material properties, normalized by density. (Longer is better. Notice the metallic materials at bottom left.) (Source)
Combine the two traits—lighter and stronger—and what we get is a material that can withstand the same load with a smaller amount of material, and the material itself weighs less for the same volume! This is a pretty neat arrangement, no?
It doesn’t end there; this is just the beginning.
–
Remember, most of the strength of a composite material comes from the fibers in the composite. Now consider a composite with all the fibers parallel to each other, i.e. pointing in the same direction. In which direction (or directions) does the composite have the most strength? Is it equally strong in all directions? Evidently not—the fibers provide tensile strength along its own direction, and so the composite itself will be much stronger in the ‘fiber direction’ as compared to other directions. We’ve discussed wood as an example before, and you’ll notice that the situation is very similar to this case of unidirectionally arranged fiber-reinforced composites.

Load on a table top: notice the fiber direction! Here the requirements are bending strength for the table top, and ability to transfer the load to the legs of the table. (Source)
Now that we’re comfortable with the idea of a unidirectional composite, consider this material as a building block. If you had a unidirectional material, that you could orient any way you like, and stack them so that the final material had fibers in multiple orientations, could you design a material to be strong in any direction you wanted? Certainly you could! And this is exactly what is done.
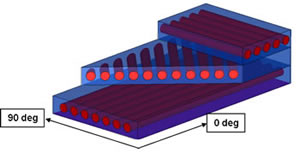
Composite Ply Layup. (Source)
And this brings us to the engineering and design side of composites. Even though, at first look, this seems like a dubious idea—isn’t it better that the things we make are equally strong in all directions? What if it breaks in one of the weaker directions?–this makes good engineering sense. Whenever a new component is designed, the designer has already figured out what the weak points of the structure are, and has already planned a way (or ways) that the component should fail, should it become overloaded or reaches the end of its life. In other words, a good engineering design factors in, during the design process, the directions that the component needs to be strong in, and the ways the material can and should fail.
Of course, this implies that the components perform at their best when they are used as intended. If a golfer strikes his golf club in frustration against a tree trunk, should he be surprised if his prized club goes out of shape? (On the other hand, if many golfers do this exact same thing, the designer of the hi-end golf club might take this into consideration when he makes a new design—but it probably will make the club even more expensive!)

A bent golf club, after it was struck against the ground. (Source)
And of course, what of the case where the component does actually need to be equally strong in all directions? Well, there’s nothing preventing the designer from using plies oriented in all directions, right? A component where the fibers are oriented so that the properties are approximately the same in all directions is called a quasi-isotropic material, i.e. a material that behaves sort of like an isotropic material, even though it actually isn’t.
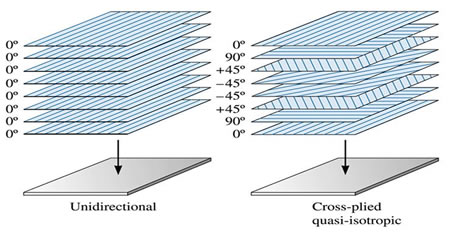
A unidirectional and a quasi-isotropic laminate. (Source)
One final thing for this session. How to describe the ply sequence of composites? In brief (I’ll clarify as we come across actual examples), the most basic nomenclature is just a sequence of the play angles, with one of the fiber directions designated the ‘zero degree’ direction. Since it can get cumbersome to write the sequences of multi-layer composites (consider a 16-ply or 32-ply laminate, for example!), symmetries and repetitions in the order of the plies is used profitably. The subscript ‘S’ denotes symmetry, ‘N’ (where N is a number) denotes N repetitions of the same order, and ‘T’ conveys that no symmetries and repetitions are present (i.e. it is the ‘total’ sequence). Please see the figure below for some examples.
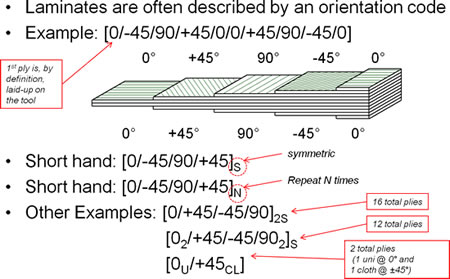
Composite stacking sequence nomenclature. (Source)
To summarize, the advantage of composites is first in its most basic properties—it is both stronger and lighter than traditional metallic materials. (It must be noted that this is a simple generalization; ‘strength’ can be of various kinds. For example, composites are usually not very good in compression). Further, composites can be engineered as per design requirements of each component. A basic unidirectional building block can be used to prepare composites with a variety of effective material properties.